25 수능 17번과 26 6월 모의고사 20번을 바탕으로 2026학년도 수능에 출제될 문제의 출제 경향을 예상해본다.
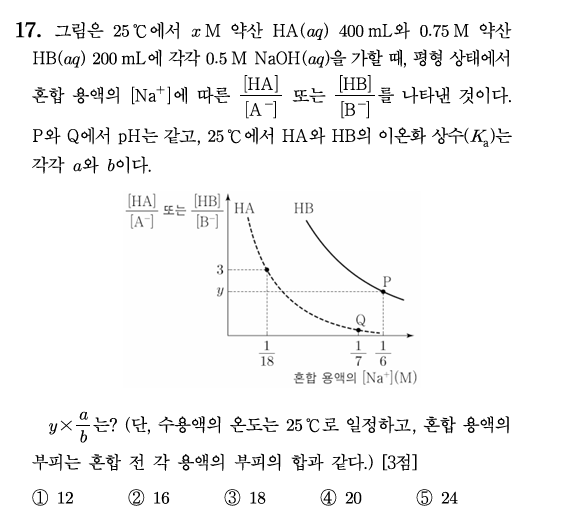
25 수능 17번
혼합 수용액의 \(\lbrack{Na}^{+}\rbrack = \frac{{Na}^{+}의\, 양}{수용액의\, 부피}\)이다. P에서 가한 \(NaOH(aq)\)의 부피를 \(V\)mL라 하면 \(\lbrack{Na}^{+}\rbrack = \frac{0.5V}{V + 400} = \frac{1}{6}\)에서 \(V = 200\)이다. 이때 \(y = \frac{\lbrack HB\rbrack}{\lbrack B^{-}\rbrack} = 2\)이다. 마찬가지로 \(\lbrack{Na}^{+}\rbrack = \frac{1}{18}\)일 때 가한 \(NaOH(aq)\)의 부피를 구하면 50mL이고, \(x = \frac{1}{4}\)이다. Q에서 \(\frac{\lbrack HA\rbrack}{\lbrack A^{-}\rbrack} = \frac{1}{4}\)이고, P와 Q에서 pH는 같으므로 \(\frac{a}{b} = \frac{Q에서\frac{\lbrack A^{-}\rbrack}{\lbrack HA\rbrack}}{P에서\,\frac{\lbrack B^{-}\rbrack}{\lbrack HB\rbrack}} = \frac{4}{\frac{1}{2}} = 8\)이다.

26 9월 모의고사 5번
혼합 수용액의 \(\lbrack{Cl}^{-}\rbrack = \frac{{Cl}^{-}의\, 양}{수용액의\, 부피}\)이다.
(가)에서 \(\lbrack{Cl}^{-}\rbrack = \frac{0.5V_{1}}{V_{1} + 400} = \frac{1}{10}\)에서 \(V_{1} = 100\)이고, 동일한 방법으로 (나)에서 \(V_{2} = 200\)이다. (가)에서 \(\frac{\lbrack{HA}^{+}\rbrack}{\lbrack A\rbrack} = \frac{1}{3}\)이므로 \(400x \times \frac{1}{4} = 0.5 \times 100\)에서 \(x = 0.5\)이다. (가)와 (나)의 pH가 같고, (나)에서 \(\frac{\lbrack{HB}^{+}\rbrack}{\lbrack B\rbrack} = \frac{1}{2}\)이므로 \(\frac{B의\, 이온화\, 상수}{A의\, 이온화\, 상수}\)=\(\frac{(나)에서\,\frac{\lbrack{HB}^{+}\rbrack}{\lbrack B\rbrack}}{(가)에서\,\frac{\lbrack{HA}^{+}\rbrack}{\lbrack A\rbrack}} = \frac{\frac{1}{2}}{\frac{1}{3}} = \frac{3}{2}\)이다.
특징점
가장 최근에 출제된 산 염기 평형 고난도 문제이다. 두 문제 모두 복잡한 계산보다는 간단한 계산의 호흡을 길게 가져가는 풀이를 요구하고 있다. 특히 기존에 제시되던 산과 염기의 비율이 아닌, 반응에 참여하지 않는 \(\lbrack{Na}^{+}\rbrack\) 또는 \(\lbrack{Cl}^{-}\rbrack\)의 값을 해석함으로써 미지수를 구해가는 형태를 취하고 있다. 따라서 해당 값에서 도출해낼 수 있는 식을 최대한 빠르게 파악하고 이후 이어지는 미지수 계산을 침착하게 처리하는 것이 문제 풀이의 핵심 요소로 볼 수 있다.
최상위권 학생들은 이뿐만 아니라 \(\frac{\lbrack{Na}^{+}\rbrack}{\lbrack HA\rbrack}\)와 같은 새로운 형태의 값이 주어질 수도 있으므로 다양한 상황과 조건에 대비하자. 이 경우 중화 반응이 모두 완료되기 전의 수용액이라면 \(\lbrack{Na}^{+}\rbrack = \lbrack A^{-}\rbrack\)이므로 우리가 익히 아는 산과 염기의 비율로 변환하여 문제를 해결할 수 있다.
