26 9월 모의고사 16번과 26 9월 모의고사 20번을 바탕으로 2026학년도 수능에 출제될 문제의 출제 경향을 예상해본다.

26 9월 모의고사 16번
(가)에서 초기 A가 8mol 존재한다고 하자. 10min일 때 \(\frac{B + C}{A} = \frac{15}{2}\)이므로 10min동안 A가 \(a\)mol 반응했다고 하고 계산해주면 \(a = 6\), 즉 (가)에서 반감기는 5min이다.
(나)에서 초기 A는 16mol 존재한다. 20min일 때 (가)에서 A는 0.5mol 존재하고 (나)에서 A는 이의 8배인 4mol이 존재하므로 (나)의 반감기는 10min이다.
(나)에서 초기 C가 \(n\)mol 존재한다고 하고 10min일 때의 조건에 대입하면 \(n = 4\)이다. 따라서 \(x = \frac{1}{4}\)이다.
(가)와 (나)에서 혼합 기체의 몰비는 2:5이고, 이는 \(\frac{PV}{T}\)의 값과 비례하므로 \(\frac{T_{2}}{T_{1}} = \frac{9}{10}\)이다.
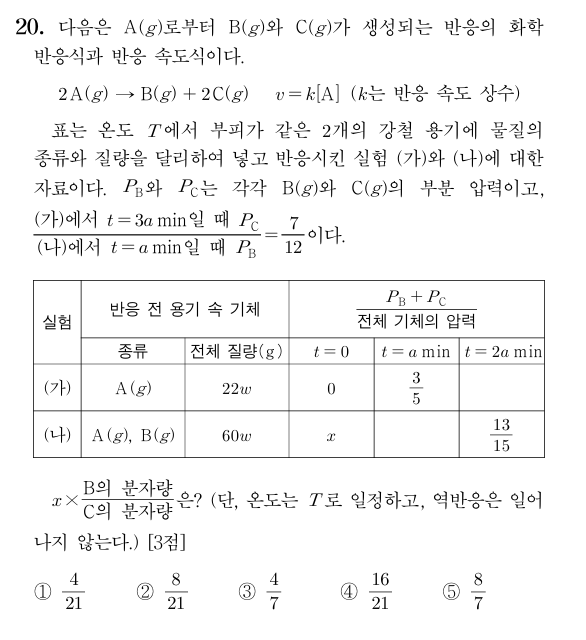
26 9월 모의고사 20번
(가)에서 \(t = amin\)일 때의 조건을 이용하면 이 반응의 반감기는 \(amin\)이다.
(가)에서 \(t = 3amin\)일 때 C의 양을 7mol이라 하면 반감기가 3번 진행된 상태이므로 초기 A 22\(w\)g의 양은 8mol이다.
(나)에서 \(t = amin\)일 때 B의 양은 12mol이고, 이때 A의 양을 4\(n\)mol이라 하면 반감기가 1번 진행된 상태이므로 C의 양 또한 4\(n\)mol이다.
반감기를 한번 더 진행시켜 주어진 조건을 활용하면 \(n = 2\)이고, 초기 A와 B의 양은 각각 16mol, 8mol이다.A 16mol은 44\(w\)g이므로 B의 질량은 16\(w\)g이고, 둘의 분자량 비는 11:8이다.
이를 화학 반응식에 대입하면 A~C의 분자량비는 11 : 8 : 7이다.
특징점
서로 다른 강철 용기에서 혼합 기체 조건을 달리하여 반응을 진행시키는 문제로, 최근에 가장 빈번하게 출제되는 반응 속도 고난도 유형이다. 이러한 문제들은 한 반응에서의 비교적 쉽게 구해지는 반감기를 나머지 한 반응에 적용하여 반응을 진행시키는 풀이가 기본 틀이므로 항상 이를 의식하여 문제에 접근하자.
반응 속도 문제에서 첫 단추를 채우는 것보다 중요한 것은 이후의 계산 과정이다. 만약 문제에서 기체의 정확한 양을 제시하지 않았다면 문제 조건에 맞게 임의로 기체의 양을 설정하여 계산량을 줄일 수 있다. 26 9월 모의고사 20번과 같이 각 강철 용기에 존재하는 기체의 비율이 조건으로 주어졌을 때 이를 기준으로 기체의 양을 설정한다면, 이후 상댓값을 문제의 실제 비율로 다시 변환하는 불필요한 과정을 생략하고 계산 실수를 최소화할 수 있다. 비슷한 상황의 문제를 23 9월 모의고사 19번 또는 23 수능 19번을 통해 충분히 연습해 두자.
또한 수능에서는 26 9월 모의고사 16번과 같이 \(PV = nRT\)를 활용하는 과정을 추가하여 난이도를 조절할 수 있으므로 최상위권 학생들은 이를 염두에 두는 것이 좋다. 23 수능 20번처럼 기체 방정식에서의 비례 관계를 이용하여 초기 미지수 값을 먼저 해결해야 하는 상황이 주어질 수도 있고, 26 6월 모의고사 19번과 같이 초기 부피를 다르게 하여 몰 농도 계산을 헷갈리게 유도할 가능성 또한 열려 있다.
특히 26 6월 모의고사 19번와 26 9월 모의고사 16번을 비교하면 전자는 두 강철 용기의 온도가 동일했고, 후자는 두 강철 용기의 부피가 달랐지만 A의 조건을 질량으로 제시하여 곧바로 계산이 가능했다. 두 문제에서 힘을 뺀 부분을 건드려 고난도 문제로 출제한다면 상당히 까다로울 수 있으니 이 점을 유의하자.
