23 수능 20번과 26 9월 모의고사 13번을 바탕으로 2026학년도 수능에 출제될 문제의 출제 경향을 예상해본다.

23 수능 20번
\(PV = nRT\)에서 압력과 온도가 같으면 기체의 양은 부피에 비례한다. (나)에서 B 4g을 1mol이라 하면 (가)에서 혼합 기체의 양은 3mol이므로 C의 양은 2mol이다. 평형 Ⅱ에서 실린더의 부피가 \(\frac{320}{7}\)L이므로 혼합 기체는 \(\frac{32}{7}\)mol 존재한다. 평형 Ⅲ에서는 실린더의 부피가 56L이고, 온도가 \(\frac{7}{6}T\)K이므로 혼합 기체는 \(\frac{24}{5}\)mol 존재한다. 반응을 전개하여 평형 상수를 구하면 각각 \(a = 1,\, b = \frac{1}{8}\)이고, 평형 Ⅰ에서 \(a = 1\)임을 이용하여 방정식을 풀면 실린더의 부피는 36L, \(x = \frac{2}{3}\)이다.
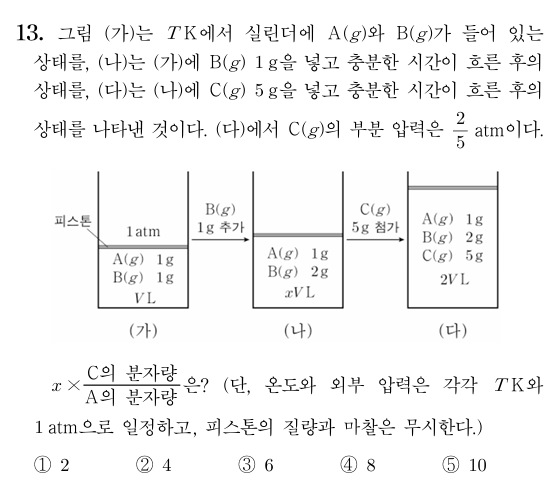
26 9월 모의고사 13번
\(PV = nRT\)에서 압력과 온도가 같으면 기체의 양은 부피에 비례한다. (다)에서 C의 부분 압력이 \(\frac{2}{5}\)atm이므로, A와 B의 부분 압력 합은 \(\frac{3}{5}\)atm이다. 즉 C의 양을 2mol이라 하면 A와 B의 양의 합이 3mol이므로 (나)와 (다)의 부피비는 3:5이고, \(x = \frac{6}{5}\)이다. (가)에서 A와 B의 양의 합이 2.5mol이므로 B 1g은 0.5mol이고, A 1g은 2mol이다. A와 C의 질량비가 1:5일 때 몰비가 1:1이므로 분자량비는 1:5이다.
특징점
단원은 다르지만 두 문제에서 모두 \(PV = nRT\)에서의 비례 관계를 통해 질량을 기체의 양으로 변환하여 접근하는 풀이를 요구하고 있다. 실린더에서 외부 압력과 온도가 일정하다면 기체의 양은 부피로 취급해도 무방하다. 즉, 23 수능 20번에서 B 4g은 10L, C 20g은 20L로 260913에서 (A 1g + B 2g)은 1.2\(V\)L, C 5g은 0.8\(V\)L로 취급하여 상댓값을 통해 계산을 편하게 가져갈 수 있다는 것이다.
26 9월 모의고사 13번에서 쓰인 이 개념이 고난도 문제와 접목되면 23 수능 20번과 같이 최고난도 문제의 풀이 과정에 등장할 수 있다. 6월과 9월의 4페이지가 비교적 평이하였다고 해서 수능도 무난히 흘러갈 것이라는 보장은 없다.
고난도 기체 문제에서는 항상 질량과 밀도를 조건으로 제시했기 때문에 이를 기체의 양으로 변환하는 풀이를 항상 의식해 두자.
최근 수능 기조는 6월 9월과 상이한 출제 유형을 보이고 있으므로 이와 같이 복잡한 상황 해석과 계산을 요구하는 고난도 문제가 오랜만에 얼굴을 비출 수도 있다.
