26 6월 모의고사 19번, 26 9월 모의고사 18번, 26 9월 모의고사 19번을 바탕으로 2026학년도 수능에 출제될 문제의 출제 경향을 예상해본다.

26 6월 모의고사 19번
전체 운동 시간 동안 \(A\)의 연직 속도 변화량의 크기가 \(\sqrt{2}v\,\)이므로, 전체 운동 시간은 \(\frac{\sqrt{2}v}{g}\)이다. \(A\), \(B\)가 \(a\), \(b\)를 지나는 시점은 전체 운동의 절반 시점이고, 상대 속도의 크기는 \(2v\,\)이므로, \(a\)와 \(b\) 사이의 거리는 \(2v \times (\frac{1}{2} \times \frac{\sqrt{2}v}{g}) = \frac{\sqrt{2}v^{2}}{g}\)이다.

26 9월 모의고사 18번
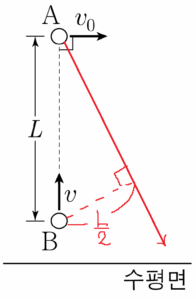
(가)에서 \(A\), \(B\)의 최소 거리가 \(\frac{L}{2}\)이므로, \(B\)의 초기 위치에서 \(B\)에 대한 \(A\)의 상대 운동 경로에 내린 수선의 발까지의 거리가 \(\frac{L}{2}\)임을 고려하면 \(v = \sqrt{3}v_{0}\)이다.
(나)에서 \(A\), \(B\)는 \(p\)에 동시에 도달하므로 \(B\)의 수평 속력은 \(v_{0}\)이고, 피타고라스 정리에 의해 연직 속력은 \(\sqrt{2}v_{0}\)이므로 \(\tan\theta = \frac{\sqrt{2}}{2}\)이다.
특징점
2026학년도 평가원에 나온 가장 어려운 난이도의 두 포물선 문항 모두 두 물체 사이의 거리에 대한 조건을 상대 속도를 이용하여 분석하는 관점을 수험생들이 이미 알고 있다는 식으로 출제되었습니다.
기존에도 당연히 이런 관점으로 접근하는 문항들은 많았으나, 이렇게 간단한 상황 설정에서도 물체 사이의 거리를 활용하여 조건을 제시하는 문항을 두 번 연속으로 냈다는 점은, 같은 소재를 쓰지는 않더라도 관점 자체를 염두에 두어야 할 것을 시사합니다.

26 9월 모의고사 19번
\(P\)에서 전기장의 \(x\,\), \(y\,\)성분의 크기가 같으므로, \(A\), \(B\)에 의한 전기장을 각각 \((3E\,,\,\, E)\), \(( – 9E\,,\,\, 3E)\)라 하면(\(\because\) 전하량 비 \(1:3\), 거리 동일) \(C\)에 의한 전기장은 \((0\,,\,\, 2E)\)가 되어야 한다.
이제 \(Q\)에서의 전기장을 \(P\)와 비교하며 구하면, \(A\)에 의한 전기장은 \(\frac{10}{4} \times \sqrt{10}E \times (1\,,\,\, 0)\), \(B\)에 의한 전기장은 \(\frac{10}{16} \times 3\sqrt{10}E \times ( – 1\,,\,\, 0)\), \(C\)에 의한 전기장은 \(\frac{16}{10} \times 2E \times ( – 1\,,\,\, 3) \times \frac{1}{\sqrt{10}}\)이다. 정리하면 \(\frac{E_{y}}{E_{x}} = \frac{192}{61}\)이다.
특징점
이렇게까지 복잡한 계산을 요구하는 문항은 개정 이래 없었습니다.
그나마 비슷한 계산량을 뽑으면 2021학년도 수능 20번 정도가 되겠네요.
점전하에 의한 전기장 문제는 신경을 쓰지 않는다면 필연적으로 숫자가 더러워지는 대신(ex. 2023학년도 수능 14번),
그만큼 어느 정도까지만 계산을 해냈다면 선지를 고르는 데에는 어렵지 않은 숫자가 나오므로 초반 부분을 실수하지 않고 정확하게 계산해낸 뒤 필요한 수, 예를 들어 분모나 분자 중 하나를 적당히 계산하여 나오는 수의 소인수 일치 여부 정도를 판단하여 선지를 고르는 극단적인 상황도 고려해봄직합니다.