25 9월 모의고사 14번과 25 수능 16번을 바탕으로 2025학년도에 출제된 문제의 출제 경향을 살펴본다.
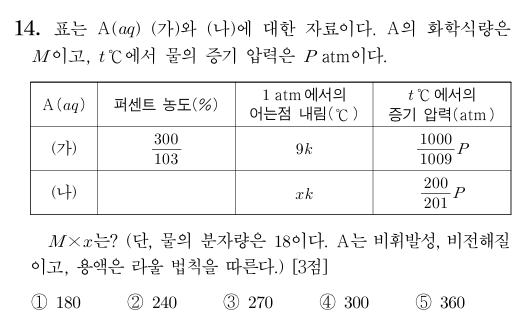
25 9월 모의고사 14번
(가)에서 물의 몰 분율은 \(\frac{1000}{1009}\)이므로 A와 물의 몰비는 9:1000이다. 퍼센트 농도가 \(\frac{300}{103}\)% 이므로 A와 물의 질량을 각각 \(a\)g, \(b\)g이라 하면 \(\frac{a}{a + b} \times 100 = \frac{300}{103}\)에서 \(a\):\(b\)=3:100이다. 질량비가 3:100, 몰비가 9:1000이므로 화학식량의 비는 10:3이고 \(M = 60\)이다. (나)에서 A와 물의 몰비는 1:200이므로 \(9:x = \frac{9}{1000}:\frac{1}{200}\)에서 \(x = 5\)이다.
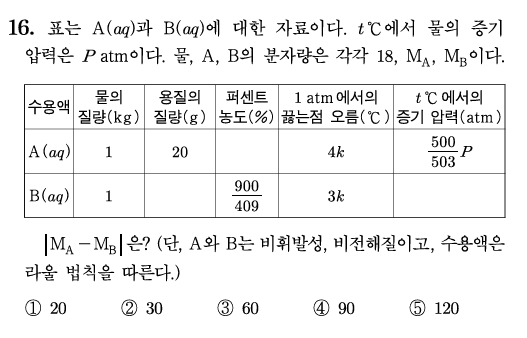
25 수능 16번
\(A(aq)\)에서 물의 몰 분율이 \(\frac{500}{503}\)이므로 A와 물의 몰비는 3:500이다. A와 물의 질량비가 1:50이므로 화학식량의 비는 10:3이다. 따라서 \(M_{A} = 60\)이다.
\(B(aq)\)에서 퍼센트 농도가 \(\frac{900}{409}\%\)이므로 B의 질량을 \(x\)g이라 하면, \(\frac{x}{1000 + x} \times 100 = \frac{900}{409}\)에서 \(x = \frac{45}{2}\)이다. \(A(aq)\)과 \(B(aq)\)에서 물의 질량은 같으므로 용질의 몰비는 끓는점 오름비인 4:3과 같고 질량비가 8:9이므로 화학식량의 비는 2:3이다. 따라서 \(M_{B} = 90\)이다.
연계 분석
- 수용액의 종류가 한 가지에서 두 가지로 늘었을 뿐 초기 조건과 구해야 하는 값이 동일한 두 문제이다. 증기 압력을 통해 용매와 용질의 몰 분율을 구하고 이를 퍼센트 농도와 연결하는 풀이를 공통적으로 요구하고 있다.
- 여기서 주목해야 할 부분은 평가원에서 채택한 숫자이다. 분자와 분모에 다소 지저분해 보이는 숫자를 채택하였다.
이는 모두 의도된 값으로, 학생들이 퍼센트 농도를 용질과 용매의 질량으로, 증기 압력 값을 용질과 용매의 양으로 나눌 수 있는지를 묻고 있다. - 따라서 최상위권 학생이라면 25 9월 모의고사 14번에서 퍼센트 농도를 \(\frac{3}{3 + 100} \times 100\)으로, 증기 압력 값을 \(\frac{1000}{9 + 1000}\)으로 분리하는 계산을 익혔어야 하며, 이를 숙지한 상태에서 25 수능 16번을 접근했다면 매우 간단하게 값을 처리하여 4 페이지 고난도 문항에 할애할 시간을 확보할 수 있었다.
- 이전까지는 용액의 총괄성 문제에서 최대한 간단한 정수값으로 분자와 분모를 구성했던 반면, 해당 문제들은 스케일이 큰 값을 취함으로써 이를 계산하는 것이 아닌, 두 물질의 몰 분율과 바로 연결 짓기를 요구하는 새로운 출제 경향을 보여주었다.
이러한 경향이 수능까지 이어질 것을 고려하여 문제의 외형뿐만 아니라 평가원이 유도하고 있는 풀이를 눈여겨보았어야 하며 이를 통해 수능에서 연계 체감도를 높일 수 있었을 것이다.
