25 6월 모의고사 20번과 25 수능 17번을 바탕으로 2025학년도에 출제된 문제의 출제 경향을 살펴본다.
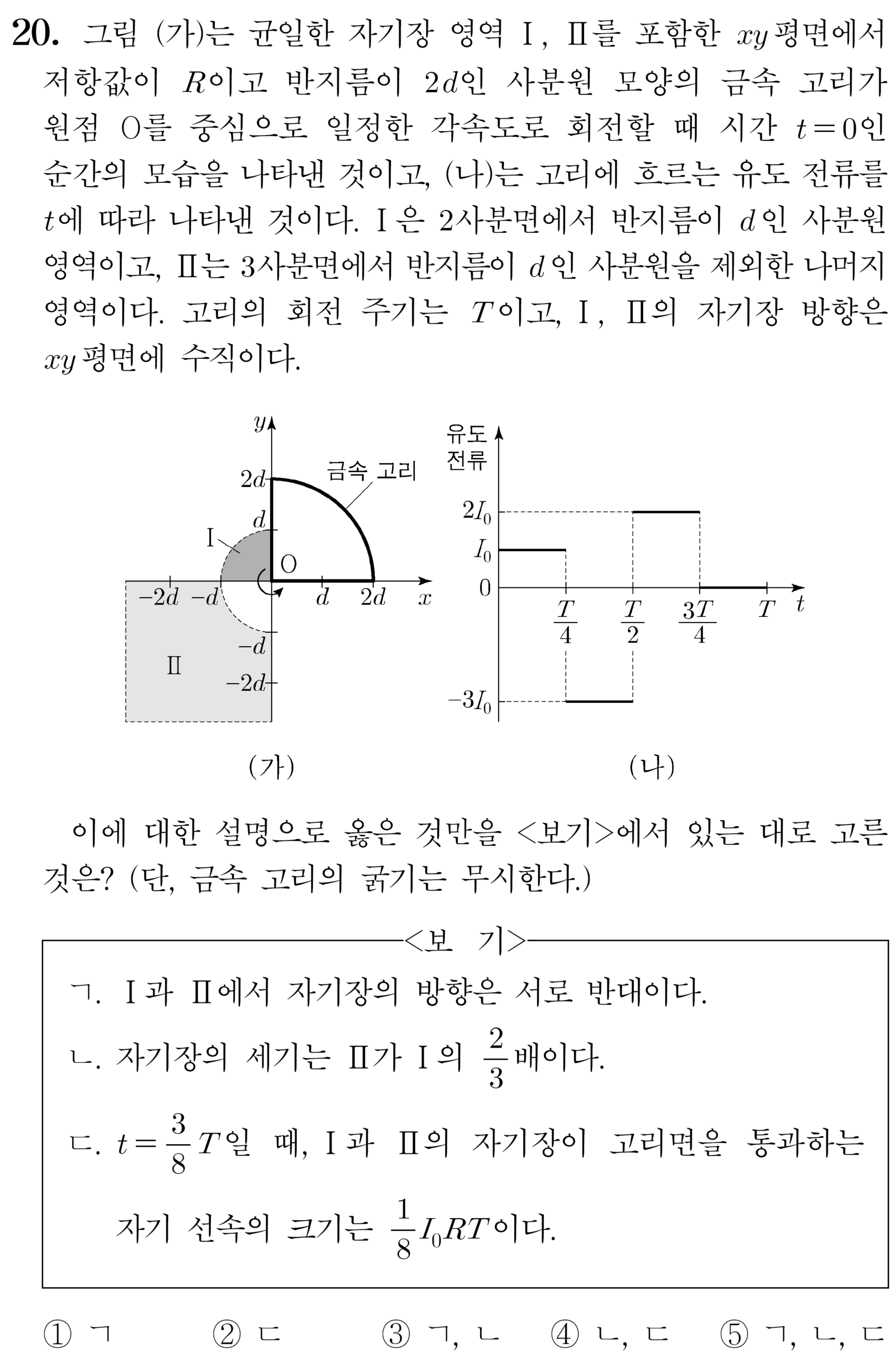
25 6월 모의고사 20번
ㄱ. Ⅰ로 들어갈 때와 Ⅱ에서 나갈 때 고리에 흐르는 유도 전류의 방향이 같으므로 Ⅰ, Ⅱ에서 자기장의 방향은 서로 반대이다. (O)
ㄴ. 이때 유도 전류의 세기비가 \(1:2\)이고 같은 시간 동안 면적의 변화량 비가 \(1:3\)이므로, Ⅰ, Ⅱ에서 자기장의 세기비는 \(3:2\)이다. (O)
ㄷ. \(\mid \Delta\Phi \mid = |\int_{}^{}\ Vdt| = |\int_{}^{}\ IRdt|\)이므로, \(t = 0\)부터 \(t = \frac{3}{8}T\,\)까지 \(|\int_{0}^{\frac{3}{8}T}\ IRdt| = \frac{1}{8}I_{0}RT\,\)에서 \(t = \frac{3}{8}T\,\)일 때 고리를 통과하는 자기 선속의 크기는 \(\frac{1}{8}I_{0}RT\,\)이다. (O)
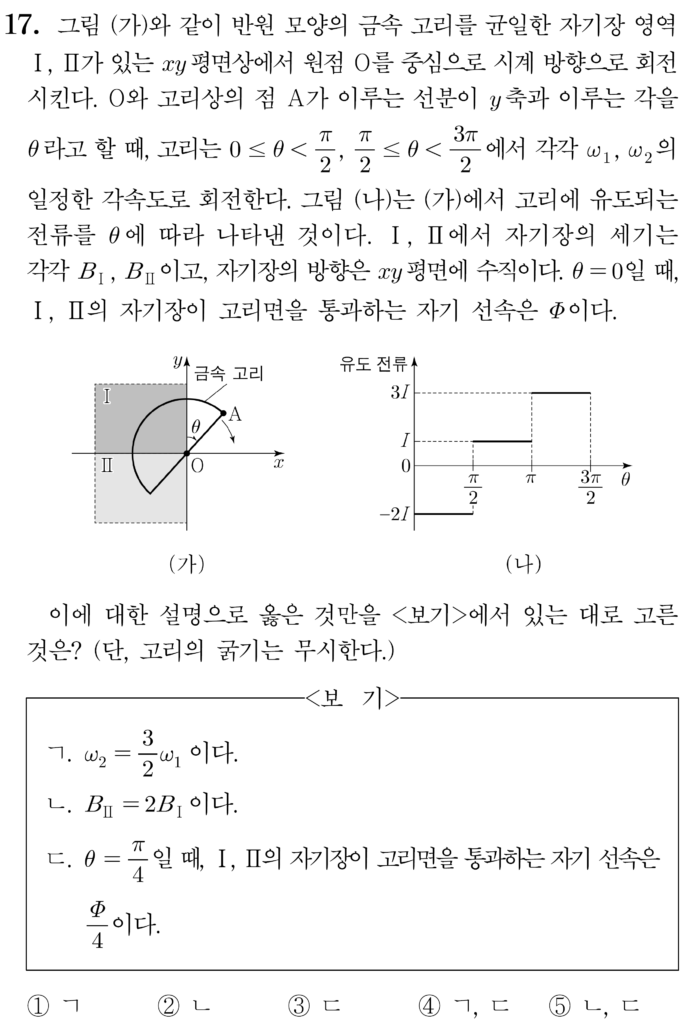
25 수능 17번
ㄱ. Ⅱ에서 나올 때와 Ⅱ에 들어갈 때 고리에 흐르는 유도 전류의 세기비는 \(2:3\)이므로 각속도의 크기비 \(\omega_{1}:\omega_{2} = 2:3\)이다. (O)
ㄴ. Ⅱ에서 나올 때와 Ⅰ에서 나올 때 고리에 흐르는 유도 전류의 세기비는 \(2:1\), 각속도의 크기비는 \(2:3\)이므로 자기장의 세기비는 Ⅱ, Ⅰ에서 \(3:1\)이다. (X)
ㄷ. \(\theta = 0\)일 때 자기 선속이 \(\Phi\)이고, \(\theta = \pi\,\)일 때 자기 선속이 \(0\)이다. 이때 \(|\Delta\Phi| = |\int_{}^{}\ Vdt| = |\int_{}^{}\ \frac{IR}{\omega}d\theta|\)이므로 \(0 \leq \theta < \frac{\pi}{2}\)에서와 \(\frac{\pi}{2} \leq \theta < \pi\,\)에서 자기 선속의 변화량의 비는 \(- 3:1\)이다.
따라서 \(\theta = \frac{\pi}{4}\)일 때 자기 선속은 \(\frac{\Phi}{4}\)이다. (O)
1. 연계
① 시각적 관점
부채꼴 모양이 금속 도선이 일정한 각속도로 회전할 때, 자기장 영역에 들어가거나 나가면서 흐르는 유도 전류를 시간 또는 각도에 따라 나타낸 자료를 제시했다는 점이 유사합니다.
선지에서 물어보고 있는 내용 또한 자기장 영역에서 자기장의 세기비, 자기장이 고리면을 통과하는 자기 선속으로 동일합니다.
➁ 해설적 관점
선지에서 물어보는 내용이 유사한 만큼, 문제를 풀기 위한 접근 방식 자체도 크게 다르지 않습니다.
유도 전류의 세기비와 방향을 가지고 자기장의 세기비와 방향을 판단하는 과정, 이 과정에서 비교를 위한 올바른 시점을 잘 골라내야 한다는 점, ㄷ. 선지에서 유도 전류가 시간 또는 각속도에 대한 그래프로 주어져 있을 때 그래프의 밑 면적을 이용할 수 있다는 점 모두 유사합니다.
2. 해당 문항이 다른 평가원 문항과 달랐던 이유
이전까지 회전하는 부채꼴 도선에 대해 ‘자기 선속의 크기’를 이런 느낌으로 계산하도록 시키는 문항은 거의 없었습니다.
2022학년도 수능 16번처럼 정지한 상태의 도선에서 \(\Phi = BA\,\) 관점을 이용하거나, 2023학년도 6월 19번처럼 패러데이 법칙을 거의 그대로 사용하는 \(|\int_{}^{}\ Vdt| = \mid \Phi \mid\) 관점이 아니라, 유도 전류 그래프가 제시되었을 때에도 이 그래프상에서 자기 선속을 \(\Phi = BA\,\)로 옮기지 않고 바로 계산할 수 있는 관점을 2025학년도 6월 20번이 제시해주고 있는 셈이죠.
\(\mid \Delta\Phi \mid = |\int_{}^{}\ Vdt| = |\int_{}^{}\ IRdt| = |\int_{}^{}\ \frac{IR}{\omega}d\theta|\)와 같은 일종의 진화 과정을 엿볼 수 있습니다.
물론 2025학년도 수능 17번의 경우 \(\Phi = BA\,\) 관점을 직접 쓰더라도 문항을 쉽게 풀 수 있지만, 비율 관계와 기하적 해석이 더 쉽다고 느끼는 학생이라면 각 시점에서의 자기 선속의 비가 주어질 때 계산이 더 쉽게 이루어질 수도 있겠습니다. 물론 검산용으로도 좋겠죠.
